Jia Wangwang

Jia Wangwang

🧐 About Me

Hi there! I am a 1-year PhD student in National University of Defense Technology (NUDT), under the supervision of Prof.Yong Dou and Prof.Kele Xu. Before that, I obtained my Academic Degree in Computer Science and Technology from Chongqing University in July, 2024.

Research Interests: Continual learning，Multi-Model Deep Learning

πŸ”₯ News

  • 2024.07: πŸŽ‰ I graduated from CQU!
  • 2025.02: πŸŽ‰ One paper is accepted by CVPR 2025!

πŸ“ Selected Publications

(* indicates equal contribution; # indicates corresponding authorship.)

CVPR 2025(CCF A)
sym

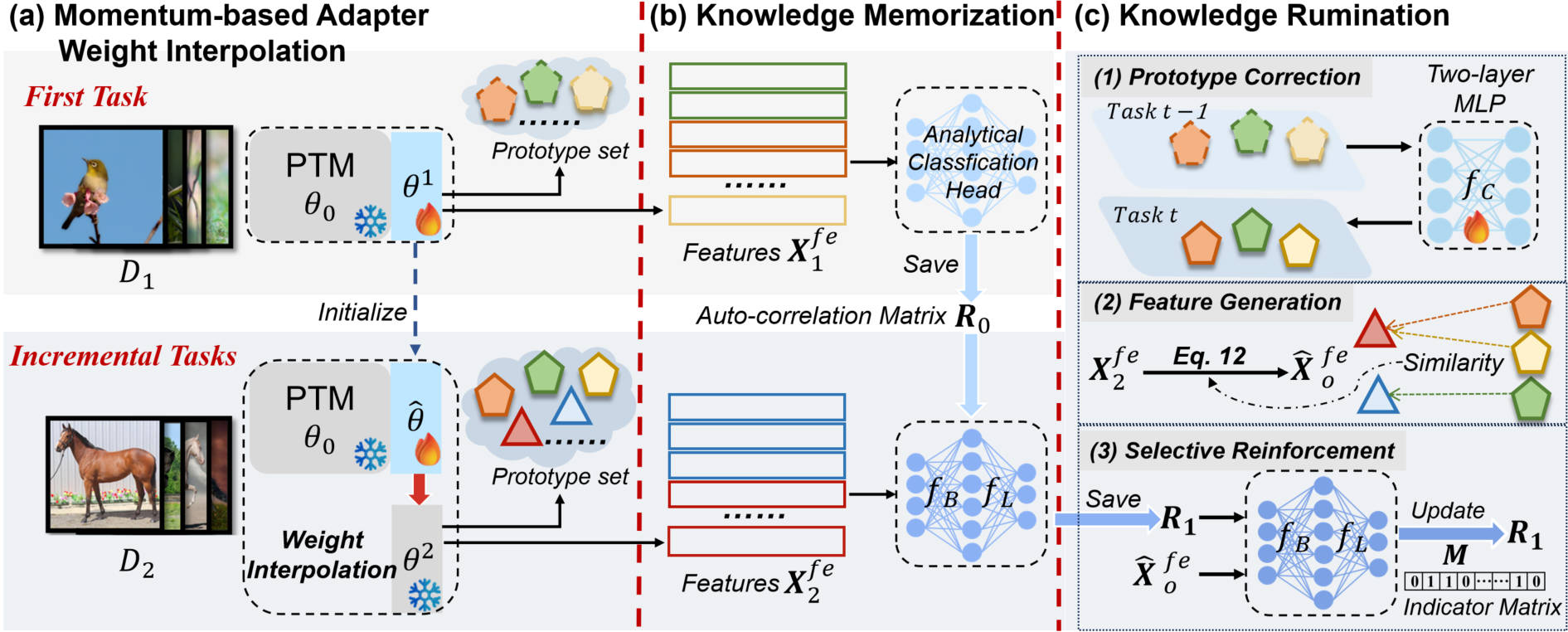
Knowledge Memorization and Rumination for Pre-trained Model-based Class-Incremental Learning code
Zijian Gao*,Wangwang Jia*, Xingxing Zhang, Dulan Zhou, Kele Xu#, Feng Dawei, Yong Dou, Xinjun Mao, Huaimin Wang. (CVPR 2025 (CCF A) )

πŸŽ– Honors and Awards

πŸ“– Educations

  • πŸŽ“ 2024.09 - β€”β€”-, PhD student,National University of Defense and Technology, China.
  • πŸŽ“ 2020.09 - 2024.07, Undergraduate, Chongqing University, China.

πŸ’¬ Services

πŸŽ™ Miscellaneous

Running

I enjoy the time running. I am always excited about exploring new running routes and challenging myself to improve my speed and endurance. It is a great way for me to stay fit and also allows me to enjoy the outdoors and clear my mind.